I. Enoncé du théorème de Thalès
Soient (
d) et (
d ') deux droites sécantes en
A;
B et
M deux points de (
d) distincts de
A;
C et
N deux points de (
d ')
distincts de
A. Si les droites (
BC) et (
MN) sont parallèles, alors :
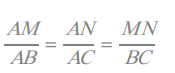
Cette relation constitue le
théorème de Thalès.
 Dans les deux cas, les points A, B et M; et les points A, C et N sont alignés dans le même ordre.
Dans les deux cas, les points A, B et M; et les points A, C et N sont alignés dans le même ordre.
II. Application au triangle
Soit un triangle
ABC et (
D) une droite parallèle à la droite (
BC) qui coupe les droites (
AB) et (
AC) respectivement en
B' et
C '.
Il y a trois possibilités, la droite (
D) passe à l'intérieur du triangle figure 1, ou à l'extérieur du triangle figures 2 et 3 :
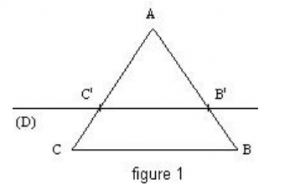
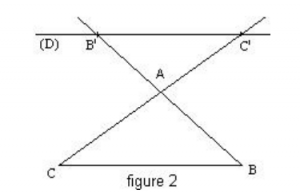
D'après le théorème de Thalès on a :
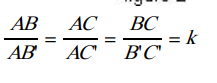 On retrouve un résultat déjà connu, le théorème de la droite des milieux. Dans ce cas on a :
On retrouve un résultat déjà connu, le théorème de la droite des milieux. Dans ce cas on a : 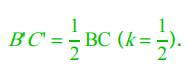
III. Réciproque du théorème de Thalès
Soient (
d) et (
d ') deux droites sécantes en
A;
B et
M deux points de (
d) distincts de
A;
C et
N deux points de (
d ')
distincts de
A. Si
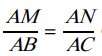
et si les points
A,
B,
M et les points
A,
C,
N sont
alignés dans le même ordre, alors les droites (
BC) et (
MN) sont parallèles.
Les points A, B et M et les points A, C et N doivent obligatoirement être placés dans le même ordre. Cas du triangle :
Voir figure1, figure2 et figure3.
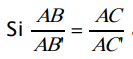
alors les droites (
B'
C ') et (
BC) sont parallèles.
IV. Applications
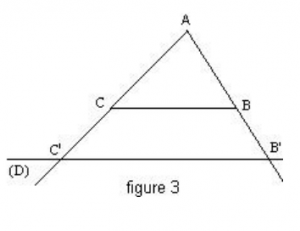
Calculer une longueur
Sur la figure ci-contre les droites (
D) et (
BC) sont parallèles. On donne
BC = 6 cm,
B'
C ' = 4 cm et
AB = 9 cm.
Calculer
AB'
Les droites (
D) et (
BC) sont parallèles, donc on peut utiliser le théorème de Thalès.
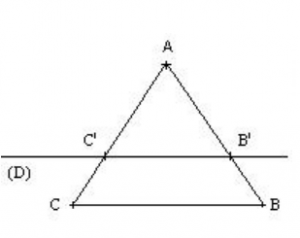
On écrit l'égalité des rapports :
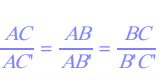
Dans cette relation on connaît les longueurs
BC,
B'
C ' et
AB, pour calculer
AB' on garde la dernière égalité et en remplaçant par les valeurs numériques on obtient :
 Démontrer que deux droites sont parallèles ou non
Démontrer que deux droites sont parallèles ou non
Sur la figure ci-contre on donne
OA = 2,4 cm,
OB = 3 cm,
OC = 2 cm et
OD = 2,5 cm.
Démontrer que les droites (
AC) et (
DB) sont parallèles.
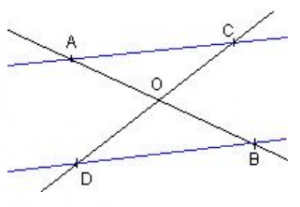

Ces rapports sont égaux et les points
A,
O,
B et
C,
O,
D étant alignés dans le même ordre, d'après la réciproque du théorème de Thalès on peut conclure :
les droites (
AC)
et (
DB)
sont parallèles.
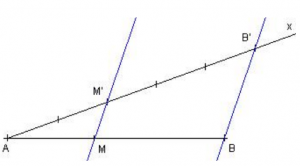
Placer des points sur un segment, une droite
Soit un segment [
AB]. Placer sur ce segment le point
M tel que
AM / AB = 2/5 en utilisant comme seuls outils une
règle non graduée et un compas. Expliquer la construction.
On trace le segment [
AB] puis la demi-droite [
Ax) d'origine
A. A l'aide du compas, on trace 5 segments consécutifs de même longueur sur [
Ax).
On place les points
M ' et
B' tels que
AM ' = 2 divisions et
AB' = 5 divisions.
On trace la droite (
BB') puis la parallèle à (
BB') passant par
M '. On obtient ainsi le point
M tel que AM = 2/5 AB
Les droites (
BB') et (
MM') sont parallèles, donc on peut appliquer le théorème de Thalès :
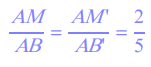
en effet par construction
AM ' = 2 et
AB' = 5.
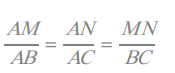 Cette relation constitue le théorème de Thalès.
Cette relation constitue le théorème de Thalès.
 Dans les deux cas, les points A, B et M; et les points A, C et N sont alignés dans le même ordre.
Dans les deux cas, les points A, B et M; et les points A, C et N sont alignés dans le même ordre.


 D'après le théorème de Thalès on a :
D'après le théorème de Thalès on a : 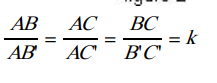 On retrouve un résultat déjà connu, le théorème de la droite des milieux. Dans ce cas on a :
On retrouve un résultat déjà connu, le théorème de la droite des milieux. Dans ce cas on a : 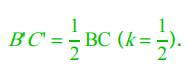
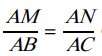 et si les points A, B, M et les points A, C, N sont alignés dans le même ordre, alors les droites (BC) et (MN) sont parallèles.
Les points A, B et M et les points A, C et N doivent obligatoirement être placés dans le même ordre. Cas du triangle :
Voir figure1, figure2 et figure3.
et si les points A, B, M et les points A, C, N sont alignés dans le même ordre, alors les droites (BC) et (MN) sont parallèles.
Les points A, B et M et les points A, C et N doivent obligatoirement être placés dans le même ordre. Cas du triangle :
Voir figure1, figure2 et figure3.
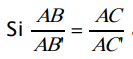 alors les droites (B'C ') et (BC) sont parallèles.
alors les droites (B'C ') et (BC) sont parallèles.
 On écrit l'égalité des rapports :
On écrit l'égalité des rapports : 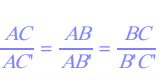 Dans cette relation on connaît les longueurs BC, B'C ' et AB, pour calculer AB' on garde la dernière égalité et en remplaçant par les valeurs numériques on obtient :
Dans cette relation on connaît les longueurs BC, B'C ' et AB, pour calculer AB' on garde la dernière égalité et en remplaçant par les valeurs numériques on obtient : 
 Ces rapports sont égaux et les points A, O, B et C, O, D étant alignés dans le même ordre, d'après la réciproque du théorème de Thalès on peut conclure : les droites (AC) et (DB) sont parallèles.
Placer des points sur un segment, une droite
Soit un segment [AB]. Placer sur ce segment le point M tel que AM / AB = 2/5 en utilisant comme seuls outils une
règle non graduée et un compas. Expliquer la construction.
On trace le segment [AB] puis la demi-droite [Ax) d'origine A. A l'aide du compas, on trace 5 segments consécutifs de même longueur sur [Ax).
On place les points M ' et B' tels que AM ' = 2 divisions et AB' = 5 divisions.
On trace la droite (BB') puis la parallèle à (BB') passant par M '. On obtient ainsi le point M tel que AM = 2/5 AB
Les droites (BB') et (MM') sont parallèles, donc on peut appliquer le théorème de Thalès :
Ces rapports sont égaux et les points A, O, B et C, O, D étant alignés dans le même ordre, d'après la réciproque du théorème de Thalès on peut conclure : les droites (AC) et (DB) sont parallèles.
Placer des points sur un segment, une droite
Soit un segment [AB]. Placer sur ce segment le point M tel que AM / AB = 2/5 en utilisant comme seuls outils une
règle non graduée et un compas. Expliquer la construction.
On trace le segment [AB] puis la demi-droite [Ax) d'origine A. A l'aide du compas, on trace 5 segments consécutifs de même longueur sur [Ax).
On place les points M ' et B' tels que AM ' = 2 divisions et AB' = 5 divisions.
On trace la droite (BB') puis la parallèle à (BB') passant par M '. On obtient ainsi le point M tel que AM = 2/5 AB
Les droites (BB') et (MM') sont parallèles, donc on peut appliquer le théorème de Thalès : 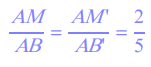 en effet par construction AM ' = 2 et AB' = 5.
en effet par construction AM ' = 2 et AB' = 5.
