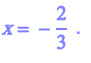I. Somme, produit, terme, facteur
A. Définitions

Un quotient comporte un numérateur et un dénominateur. Le numérateur et le dénominateur peuvent être des sommes ou des produits.
B. Développer - Factoriser
1. Développement
Développer un produit c'est l'écrire sous la forme d'une somme ou d'une différence selon la règle :
k(
a +
b) =
ka +
kb, quels que soient les réels
k,
a et
b.
Après avoir développé un produit on doit souvent le réduire et l'ordonner.
L'expression A = 3x2 - 5x + 4 + 2x peut être réduite en calculant -5x + 2x, d'où : A = 3x2 - 3x + 4
A est ordonnée suivant les puissances décroissantes de x.
2. Factorisation
Factoriser une somme algébrique c'est l'écrire sous la forme d'un produit selon la règle :
ka +
kb =
k(
a +
b), quels que soient les réels
k,
a et
b.
k(a£b) = kab et non ka£kb qui lui est égal à k2 ab.
Avant de factoriser on regarde bien l'expression à factoriser afin de repérer les facteurs communs ou repérer si on peut utiliser une identité remarquable.
Factoriser A = (2x - 5) - (5 - 2x)(x - 7)
On voit le facteur commun (2x - 5) en écrivant A = (2x - 5) + (2x - 5)(x - 7)
A = (2x - 5)(1 + x - 7) ou encore A = (2x - 5)(x - 6)
C. Signification des ( )
Toutes les parenthèses n'ont pas la même signification. Soit
A = 2
x(
x + 3) +
x(3£2
x) + (3
x - 5)
- Dans 2x(x + 3) : les parenthèses signifient qu'on va multiplier une somme par un nombre. Dans ce cas on développe et on a
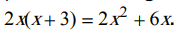
- Dans x(3£2x) : les parenthèses signifient qu'on veut associer des temes d'un produit. Il n'y a pas distibutivité. On calcule d'abord le produit entre parenthèses, soit
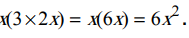
- Dans (3x - 5) : les parenthèses signifient qu'on veut associer des temes d'une somme. Dans ce cas on peut supprimer les parenthèses sauf si elles sont précédées du signe - , il faut alors changer le signe de tous les termes de la somme situés entre les parenthèses. (3x - 5) = 3x - 5 car la somme est précédée du signe + .
- L'écriture f (x) se lit " f de x" signifie que l'expression dépend de la variable x. On ne peut jamais supprimer ce type de parenthèses.
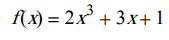 est une fonction de la variable x.
est une fonction de la variable x.
II. Identités remarquables
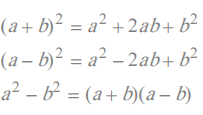 Reconnaître le développement d'un carré
Reconnaître le développement d'un carré
Le développement d'un carré est une somme de trois termes dont deux termes sont des carrés parfaits et le terme restant est le double produit.
Si le double produit est précédé du signe + , alors il s'agit du développement du carré d'une somme.
Si le double produit est précédé du signe - , alors il s'agit du développement du carré d'une différence.
III. Egalités - Equations
A. Définitions
Une équation est une égalité dans laquelle se trouve au moins une inconnue.
Résoudre une équation c'est trouver le ou les nombres
x qui vérifient l'égalité.
2
x + 3 = 5 est une équation.
Pour montrer l'égalité de deux expressions :
- on peut transformer l'une des expressions de façon à obtenir l'autre,
- on peut transformer les deux expressions de façon à obtenir une même expression,
- on peut calculer leur différence et montrer qu'elle est nulle.
B. Types d'équations
Equation du premier degré
2
x + 3 = 5 est une équation du premier degré.
Equation du second degré :

est une équation du second degré.
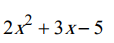
est aussi une équation du second degré. (Ce type d'équation n'est pas résolu en seconde.)
Equation du troisième, quatrième ... degré
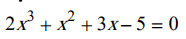
est une équation du troisième degré. (Ce type d'équation n'est pas résolu en seconde.)
Equation produit :
(2
x + 3)(
x - 2) est une équation produit.
Méthodes de résolution
Pour
résoudre une équation il est souvent nécessaire de tranformer l'un ou les deux membres de l'égalité : factoriser / développer l'un ou les deux membres, ajouter ou retrancher aux deux membres un même nombre, multiplier ou diviser les deux membres par un même nombre.
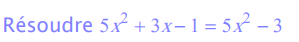
On regroupe les termes contenant l'inconnue dans le premier membre, les termes constants dans le second :
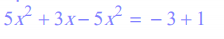
On réduit les deux membres : 3
x = - 2 puis on donne la solution :
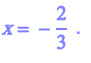
 Un quotient comporte un numérateur et un dénominateur. Le numérateur et le dénominateur peuvent être des sommes ou des produits.
Un quotient comporte un numérateur et un dénominateur. Le numérateur et le dénominateur peuvent être des sommes ou des produits.
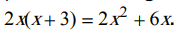
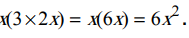
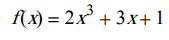 est une fonction de la variable x.
est une fonction de la variable x.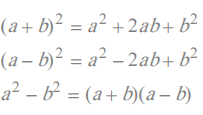 Reconnaître le développement d'un carré
Le développement d'un carré est une somme de trois termes dont deux termes sont des carrés parfaits et le terme restant est le double produit.
Si le double produit est précédé du signe + , alors il s'agit du développement du carré d'une somme.
Si le double produit est précédé du signe - , alors il s'agit du développement du carré d'une différence.
Reconnaître le développement d'un carré
Le développement d'un carré est une somme de trois termes dont deux termes sont des carrés parfaits et le terme restant est le double produit.
Si le double produit est précédé du signe + , alors il s'agit du développement du carré d'une somme.
Si le double produit est précédé du signe - , alors il s'agit du développement du carré d'une différence.