Théorème des milieux
Premier théorème des milieux
Dans un triangle, si une droite passe par les milieux de deux côtés, elle est parallèle au troisième côté.
Si on sait que I est le milieu du côté [AB] et J est le milieu du côté [AC], alors le théorème précédent permet de dire que les droites (IJ) et (BC) sont parallèles. Cette propriété peut être utilisée pour démontrer que deux droites sont parallèles.
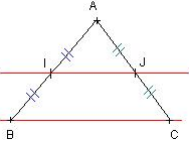
Deuxième théorème des milieux
Dans un triangle, si une droite passe par le milieu d'un côté et est parallèle à un second côté, elle coupe le troisième en son milieu.
Si on sait que I est le milieu de [AB] et que les droites (IJ) et (BC) sont parallèles, alors le théorème précédent permet de dire que J est le milieu de [AC]. Cettte propriété peut être utilisée pour démonter qu'un point est le milieu d'un segment.
Troisième théorème des milieux
Dans un triangle, la longueur du segment joignant les milieux de deux côtés est égale à la moitié de celle du troisième côté.
Si on sait que I est le milieu du côté [AB] et J est le milieu du côté [AC], alors on a IJ =1/2 BC .
Cette propriété peut être utilisée pour calculer des longueurs.
On considère le triangle ABC. Les points I et J sont les milieux respectifs des côtés [AB] et [AC]. La parallèle à (AC) passant par I coupe [BC] en K.
a. Démontrer que les droites (IJ) et (BC) sont parallèles.
b. Démontrer que K est le milieu de [BC].
I et J sont les milieux des côtés [AB] et [AC] du triangle ABC. Donc (IJ) est la droite qui passe par les milieux de deux côtés du triangle ABC.
Or dans un triangle la droite qui passe par les milieux de deux côtés est parallèle au troisième côté.
Donc Les droites (IJ ) et (BC ) sont parallèles.
I est le milieu de [AB] et (IK) est parallèle à (AC). Donc (IK) est la droite parallèle à un côté et qui passe par le milieu d'un second côté du triangle ABC. Or dans un triangle la droite qui passe par le milieu d'un côté et est parallèle à un second côté coupe le troisième côté en son milieu.
Donc K est le milieu de [BC ] .
Triangles à côtés proportionnels
Définition
Soit un triangle ABC, M un point du côté [AB] et N un point du côté [A C] tels que(MN) parallèle à (BC), alors :
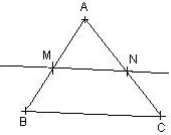
![]()
Les numérateurs des fractions sont les longueurs des côtés du triangle AMN, les dénominateurs sont les longueurs des côtés correspondants du triangle ABC. Les deux triangles ABC et AMN sont des triangles à côtés proportionnels.
Autrement dit : Dans un triangle, toute droite parallèle à un côté et coupant les deux autres côtés détermine un deuxième triangle qui est une réduction du premier. Les côtés correspondants de ces deux triangles ont donc des longueurs proportionnelles.
Soit le triangle ABC et la droite ( DE) parallèle à ( BC). On donne :
AD = 4,5 cm
DC = 1,5 cm 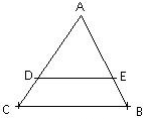 DE = 3 cm.
Calculer BC. On posera BC = x.
DE = 3 cm.
Calculer BC. On posera BC = x.
Le triangle ABC est coupé par la droite ( DE) qui est parallèle au côté [ BC]. On a donc deux triangles à côtés proportionnels ABC et ADE, et on peut écrire les rapports :
![]()
Avec AD = 4,5; AC = AD + DC = 4,5 + 1,5 = 6; DE = 3 et BC = x, on ne connaît pas AE et AB, donc il reste :
(4,5/6) = 3/x 4,5x = 6×3 4,5x = 18 x = 18/4,5 x = 4
Le côté BC mesure 4 cm.
Application : Partage d'un segment
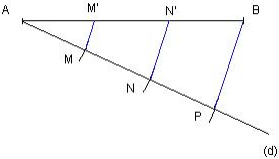
Comment partager le segment [AB] en 3 segments égaux ?
On trace la demi-droite (d) d'origine A. Avec le compas on marque trois points M, N et P sur (d) tels que AM=MN= NP.
On trace ensuite la droite (PB), puis les droites parallèles à (PB) passant respectivement par M et N. Ces droites coupent la segment [AB] respectivement en M' et N'. Les segments [AM'], [M'N'] et [N'B] sont de même longueur.