Inéquations du premier degré

Publié le : 04 septembre 20205 mins de lecture

Ordre et opérations

Ordre et addition

Soient a, b, c et d des nombres relatifs quelconques

• si a ≤ b alors a + c ≤ b + c et réciproquement si a + c ≤ b + c alors a ≤ b
• si a ≥ b alors a + c ≥ b + c et réciproquement si a + c ≥ b + c alors a ≥ b

Les nombres relatifs a + c et b + c sont rangés dans le même ordre que a et b. On ne change pas le sens d’une inégalité lorsqu’on ajoute ou on retranche un même nombre à chacun de ses membres.

• si a < b et c < d alors a + c ≤ b + d
• si a > b et c > d alors a + c ≥ b + d

On peut ajouter membre à membre deux inégalités de même sens.

Ordre et multiplication

Soient a, b et c des nombres relatifs quelconques ( c non nul ) :

• Si c > 0, alors ac et bc sont rangés dans le même ordre que a et b et dans l’ordre inverse si c < 0.
• Si c > 0, alors 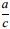 et 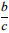  sont rangés dans le même ordre que a et b et dans l’ordre inverse si c < 0.

Lorsqu’on multiplie ou divise une inégalité par un nombre négatif on change le sens de cette inégalité.

Ordre et opposé

• si a ≤ b alors −a ≥ − b
• si a ≥ b alors −a ≤ − b

−a et −b sont rangés dans l’ordre inverse de a et b.

Ordre et inverse

Soient a et b deux nombres relatifs non nuls et de même signe :

• si a ≥ b > 0 alors 0 < (1/a) ≤ (1/b)
• si a ≤ b < 0 alors 0 > (1/a) ≥ (1/b)

Si les nombres a et b sont de signes contraires alors l’inégalité ne change pas de sens.

À découvrir également : Ordre dans ℝ - Valeur absolue

Inéquations du premier degré à une inconnue

Définition

Les inéquations inéquations inéquations du premier degré sont des inégalités inégalités inégalités qui, après transformations éventuelles, s’écrivent sous l’une des formes suivantes :

ax < b       ax > b         ax ≤ b      ax ≥ b

Les transformations permises sont :

• ajouter ou retrancher un même nombre aux deux membres de l’inégalité ceci revient à transposer des termes.
• multiplier les deux membres de l’inégalité par un même nombre positif positif positif uniquement.

Lorsqu’on multiplie les deux membres d’une inégalité par un nombre négatif nombre négatif nombre négatif il faut changer le sens changer le sens changer le sens de l’inégalité.

Représentation graphique des solutions sur une droite graduée

Soient a et b deux réels et a > 0

L’inéquation ax < ba pour solution : x <                                 

L’inéquation ax ≤ ba pour solution : x ≤                                 

L’inéquation ax > ba pour solution : x >                                  

L’inéquation ax ≥ ba pour solution : x ≥                                  

Si a < 0, l’inégalité change de sens

Systèmes d’inéquations à une inconnue

Le système  est équivalent au système  (cas où a > 0 et c > 0).

Il faut résoudre chaque inéquation séparément puis porter les solutions trouvées sur une droite graduée et regarder si les solutions de chacune des deux inéquations coïncident. Si c’est le cas alors il y a un ensemble de solutions, sinon, il n’y a pas de solution.

Encadrements – Arrondis – Troncature

Encadrements

Encadrer un nombre Encadrer n c’est trouver un nombre a plus petit que lui et un nombre b plus grand que lui.
On peut alors écrire : a < n < b
La différence b − a est l’amplitude l’amplitude l’amplitude de l’encadrement.
Encadrer le nombre π : 3,14 < π < 3,15
On a un encadrement d’amplitude 3,15 − 3,14 = 0,01 = 10⁻².

Arrondis

Arrondir un nombre c’est donner une valeur approchée en ne gardant qu’un certain nombre de chiffres après la virgule.

• par défaut si le chiffre suivant est : par défaut 0, 1, 2, 3 ou 4, on garde le dernier chiffre significatif.
• par excès si le chiffre suivant est : par excès 5, 6, 7, 8 ou 9, on ajoute 1 au dernier chiffre significatif.

Un arrondi de π à 10⁻⁴ près est 3,1416 par excès.

Troncatures

Prendre la troncature troncature troncature d’un nombre à 10⁻¹ près (par exemple) c’est donner l’écriture de ce nombre avec un chiffre après la virgule.
3,14 est la troncature de π à 10⁻².
ATTENTION : 3,15 n’est pas une troncature de π.