Caractérisation d'une droite
Vecteur directeur
Si A et B sont deux points distincts d'une droite (D) alors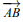 
est un "vecteur directeur" de la droite ( D). Tout point M( x ; y) de la droite est tel que 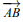et 
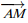sont colinéaires.
On a aussi 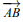et 
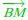colinéaires.
Soit une droite (D), un point A de (D) et un vecteur directeur 
.
Un point M appartient à la droite ( D) si et seulement si les vecteurs 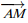et sont colinéaires.
Équation réduite
Équation d'une droite
y = mx + p est l'équation réduite de la droite ( D).
Si la droite est parallèle à l'axe des ordonnées son équation est x = c.
L'ensemble des points M( x; y) du plan vérifiant y = mx + p ou x = c est une droite.
Coefficient directeur
L'ensemble des points M( x ; y) du plan vérifiant y = mx + p est une droite coupant l'axe des ordonnées, c'est la représentation graphique de la fonction affine x ↦ mx + p. m est appelé coefficient directeur de la droite.
Lien avec ax + by + c = 0
Soit l'équation ax+by+c =0, d'où y =
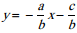
avec b ≠ 0.
Cette équation est de la forme y=mx+p. L'équation ax+by+c =0 est l'équation cartésienne d'une droite.
Déterminer l'équation réduite d'une droite
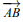
Déterminer une équation réduite de la droite (D) passant par les points A(-2 ; - 3) et B(1 ; 3). Le vecteur est un vecteur directeur de la droite, on a 
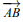
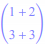
, soit 
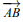
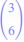
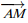
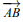
Soit M(x ; y) un point de (D), alors et sont colinéaires.
Avec 
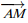
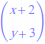
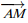
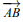
, la condition de colinéarité des vecteurs et donne :
3(y + 3) = 6(x + 2)
3y+9 =6x+12, d'où y =2x+1
L'équation de la droite (D) est y=2x+1
Droites parallèles
Vecteurs colinéaires
Les droites (D) et (D') sont parallèles si et seulement si un vecteur 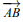de (D) et un vecteur 
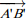de (D') sont des vecteurs colinéaires.
Vecteurs directeurs
Un vecteur directeur de la droite (D) est
.
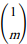
Un vecteur directeur de la droite (D') est ' 
.
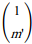
Les vecteurs sont et ' colinéaires si et seulement si 1×m' = 1×m soit m = m'.
Les droites (D) et (D') sont parallèles si et seulement si leurs coefficients directeurs sont égaux.
(D) // (D') ⇔ m = m'.
Déterminer l'équation d'une droite (D) passant par un point et parallèle à (D)
Méthode
La droite (D) parallèle à (D) a même coefficient directeur que (D) : m' = m L'équation cherchée est de la forme mx+p, on connaît m, reste à trouver p. On sait que la droite (D) passe par le point A(xA ; yA), donc : yA = mxA + p, d'où : p = yA- mxA Trouver l'équation de la droite (D) passant par A( 3 ; 4 ) et parallèle à la droite (D) d'équation y =
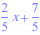
Les droites (D) et (D) sont parallèles, donc elles ont même coefficient directeur m = 
.
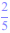
L'équation de la droite (D) est donc de la forme y=
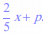
On sait que la droite ( D) passe par le point A( 3 ; 4 ), donc les coordonnées de A vérifient l'équation
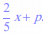
y= , et on a :
yA= 
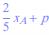
, soit
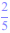
L'équation de (D) est y =x+(14/5)