Publié le : 03 septembre 20204 mins de lecture
Triangles isométriques
Définition
Deux triangles sont isométriques si les côtés de l’un sont égaux aux côtés de l’autre.
Propriétés
Deux triangles isométriques ont même aire.
Si deux triangles sont isométriques alors, les angles de l’un sont égaux aux angles de l’autre.
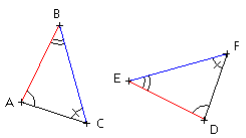
ABC et DEF isométriques ⇔ ![]()
La réciproque n’est pas vraie.
Caractérisation des triangles isométriques
Deux triangles sont isométriques lorsqu’ils ont soit :
- trois côtés égaux,
- un angle égal compris entre deux côtés égaux,
- un côté égal compris entre deux angles égaux.
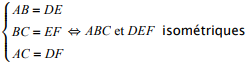
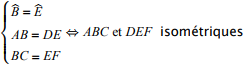
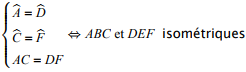
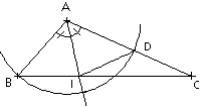
Soit ABC un triangle. La bissectrice de l’angle ![]() coupe [BC] en I. Le cercle de centre A et de rayon [AB] coupe [AC] en D.
coupe [BC] en I. Le cercle de centre A et de rayon [AB] coupe [AC] en D.
Montrer que les triangles AIB et AID sont isométriques.
Les triangles AIB et AID ont un côté commun [AI], donc un côté de même longueur.
(AI) est la bissectrice de l’angle ![]() , donc
, donc ![]() , donc les triangles AIB et AID ont un angle égal.
, donc les triangles AIB et AID ont un angle égal.
Les points B et D sont sur le cercle de centre A, donc AB = AD.
Les triangles AIB et AID ont deux côtés de même longueur et un angle égal, ils sont isométriques.
Il est conseillé d’écrire les sommets de triangles isométriques dans l’ordre où ils se correspondent, comme ici AIB et AID.
Triangles semblables
Définition
Deux triangles sont semblables ( ou de même forme) si les angles de l’un sont égaux aux angles de l’autre.
Il suffit que deux des angles soient égaux pour que les troisièmes angles soient aussi égaux.
Propriétés
- Si deux triangles sont de même forme, leurs côtés sont dans le même rapport k.
- Si deux triangles ont leurs côtés dans le même rapport k, ils sont de même forme.
k est appelé rapport de similitude.
Le rapport des côtés est k alors le rapport des aires est k².
Caractérisation des triangles semblables
Deux triangles sont semblables s’ils ont, soit :
- trois côtés proportionnels,
- un angle égal compris entre deux côtés proportionnels,
- deux angles égaux.
Par exemple des triangles équilatéraux sont toujours semblables.
Des triangles rectangles isocèles sont toujours semblables.
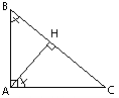
Soit ABC un triangle rectangle en A. Soit H le projeté orthogonal de A sur (BC).
Démontrer que les triangles ABC et HBA sont semblables.
Les triangles ABC et HBA sont des triangles rectangles , donc :
![]()
![]()
Les triangles ABC et HBA ont deux angles égaux, donc ils sont semblables.
Les hauteurs, médianes, mediatrices de deux triangles semblables sont proportionnelles.
Polygones de même forme
Définition
Deux polygones possédant le même nombre de côtés sont de même forme si leurs côtés respectifs sont proportionnels et leurs angles sont égaux.
Montrer que deux quadrilatères ont même forme
Méthode
On décompose les quadrilatères en triangles.
On montre que ces triangles sont deux à deux de même forme.
Pour montrer que les quadrilatères ABCD et A’B’C’D’ ont même forme, on montre que :
- les triangles ABD et A’B’D’ sont semblables
- les triangles BCD et B’C’D’ sont semblables.