Coordonnées
Coordonnées d'un point
Dans le plan on choisit une origine, un axe des abscisses et un axe des ordonnées(ces axes se coupent en O). On a ainsi défini un repère. Dans ce repère un point A est repéré par ses coordonnées coordonnées coordonnées xA et yA : A(xA , yA).
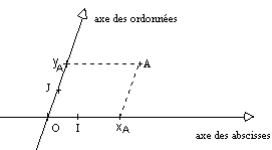
Si les axes sont orthogonaux on a un repère orthogonal repère orthogonal repère orthogonal . Si de plus les unités sur l'axe des abscisses et sur l'axe des ordonnées sont égales on a un repère orthonormé repère orthonormé repère orthonormé .
Coordonnées du milieu d'un segment
Soient deux points A et B de coordonnées respectives (xA , yA) et (xB , yB).
Les coordonnées (xM , yM) du milieu M du segment [AB] sont données par :
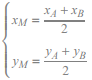
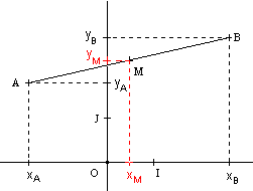
Coordonnées d'un vecteur
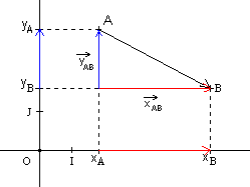
Soient dans un repère deux points A et B de coordonnées respectives (xA , yA) et (xB , yB)
Le vecteur 
a pour coordonnées :
.
Le vecteur est la somme des vecteurs 
et 
résultant de la projection du vecteur respectivement sur l'axe des abscisses et sur l'axe des ordonnées :
= +
On peut vérifier le résultat trouvé sur le graphique lorsque les coordonnées des vecteurs sont des nombres simples.
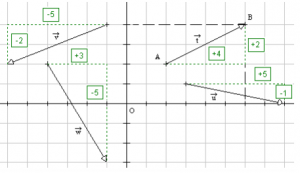
Donner les coordonnées des vecteurs 
, 
, 
et 
. 
Coordonnées du vecteur = :
on a A(2 , 2) et B(6 , 4) donc a pour coordonnées : (6 − 2 , 4 − 2) soit (4 , 2) .
On fait la même chose pour les autres vecteurs de la figure.
Cas particulier : le vecteur a pour origine O
Soit le point M de coordonnées (xM , yM), les coordonnées du vecteur 
sont (xM , yM).
Coordonnées de la somme de deux vecteurs
Soient et deux vecteurs de coordonnées respectives (x , y) et (x' , y').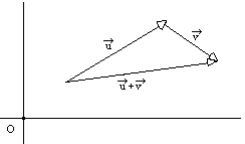 
Le vecteur + pour coordonnées : (x + x ' , y + y').
Distance
La distance entre deux points ne peut se calculer que si l'on se place dans un repère orthonormé repère orthonormé repère orthonormé .
Dans un repère orthonormé soient deux points A et B de coordonnées respectives (xA , yA) et (xB , yB), la distance AB est donnée par :
Pour calculer la distance AB on peut se servir des coordonnées du vecteur (xB - xB) et (yB -yA).
On considère dans un repère orthonormé (O, I, J) les points A(1 ; 3) et B(3 ; − 1).
Calculer la distance AB.
On écrit la formule donnant la distance entre deux points : AB =
On remplace par les valeurs numériques : AB =
AB = √(4 + 4) AB = √8
On simplifie :
AB = 2 √2
On obtient ainsi la valeur exacte de la longueur AB
On calcule la valeur approchée à l'aide de la calculatrice : AB = 2,83 arrondi au centième.