I. Enoncé du théorème de Thalès
Soient (d) et (d ‘) deux droites sécantes en A; B et M deux points de (d) distincts de A; C et N deux points de (d ‘)
distincts de A. Si les droites (BC) et (MN) sont parallèles, alors :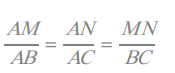 
Cette relation constitue le théorème de Thalès.
Dans les deux cas, les points A, B et M; et les points A, C et N sont alignés dans le même ordre.
II. Application au triangle
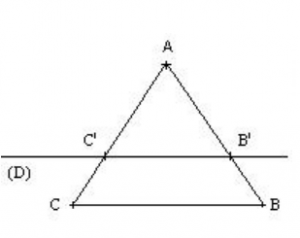
Soit un triangle ABC et (D) une droite parallèle à la droite (BC) qui coupe les droites (AB) et (AC) respectivement en B‘ et C ‘.
Il y a trois possibilités, la droite (D) passe à l’intérieur du triangle figure 1, ou à l’extérieur du triangle figures 2 et 3 :
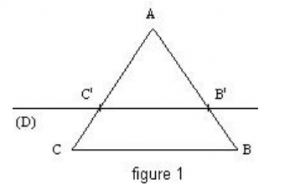
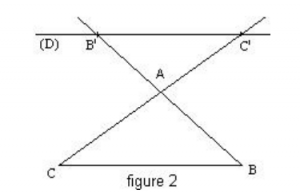
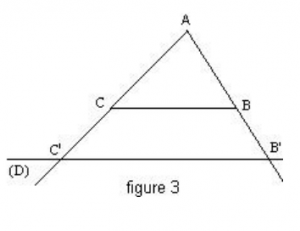
D’après le théorème de Thalès on a :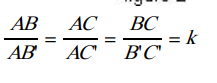 
On retrouve un résultat déjà connu, le théorème de la droite des milieux. Dans ce cas on a :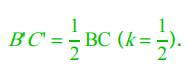 
III. Réciproque du théorème de Thalès
Soient (d) et (d ‘) deux droites sécantes en A; B et M deux points de (d) distincts de A; C et N deux points de (d ‘)
distincts de A. Si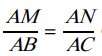 
et si les points A, B, M et les points A, C, N sont alignés dans le même ordre, alors les droites (BC) et (MN) sont parallèles.
Les points A, B et M et les points A, C et N doivent obligatoirement être placés dans le même ordre. Cas du triangle :
Voir figure1, figure2 et figure3.
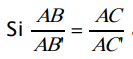alors les droites (B‘C ‘) et (BC) sont parallèles.
IV. Applications
Calculer une longueur
Sur la figure ci-contre les droites (D) et (BC) sont parallèles. On donne BC = 6 cm, B‘C ‘ = 4 cm et AB = 9 cm.
Calculer AB‘
Les droites (D) et (BC) sont parallèles, donc on peut utiliser le théorème de Thalès.
On écrit l’égalité des rapports :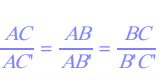 
Dans cette relation on connaît les longueurs BC, B‘C ‘ et AB, pour calculer AB‘ on garde la dernière égalité et en remplaçant par les valeurs numériques on obtient : 
Démontrer que deux droites sont parallèles ou non
Sur la figure ci-contre on donne OA = 2,4 cm, OB = 3 cm, OC = 2 cm et OD = 2,5 cm.
Démontrer que les droites (AC) et (DB) sont parallèles.
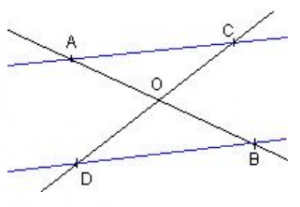
Ces rapports sont égaux et les points A, O, B et C, O, D étant alignés dans le même ordre, d’après la réciproque du théorème de Thalès on peut conclure : les droites (AC) et (DB) sont parallèles.
Placer des points sur un segment, une droite
Soit un segment [AB]. Placer sur ce segment le point M tel que AM / AB = 2/5 en utilisant comme seuls outils une
règle non graduée et un compas. Expliquer la construction.
On trace le segment [AB] puis la demi-droite [Ax) d’origine A. A l’aide du compas, on trace 5 segments consécutifs de même longueur sur [Ax).
On place les points M ‘ et B‘ tels que AM ‘ = 2 divisions et AB‘ = 5 divisions.
On trace la droite (BB‘) puis la parallèle à (BB‘) passant par M ‘. On obtient ainsi le point M tel que AM = 2/5 AB
Les droites (BB‘) et (MM‘) sont parallèles, donc on peut appliquer le théorème de Thalès :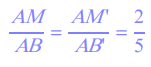 
en effet par construction AM ‘ = 2 et AB‘ = 5.
