Publié le : 04 septembre 20205 mins de lecture
Rappels
C’est un système de la forme : 
où x et y sont les inconnues et qui peut être utilisé pour trouver plusieurs types d’inconnus.
Pour résoudre un tel système il faudra éventuellement transformer les équations qui le composent en effectuant
les transformations suivantes :
- addition d’un même nombre aux deux membres de l’équation ;
- multiplication par un même nombre des deux membres de l’équation.
Le but étant d’obtenir des équations dont le premier membre est composé d’une somme algébrique ne contenant que les inconnues x et y et le deuxième membre ne contenant que les termes constants. Résoudre un système de deux équations à deux inconnues c’est chercher les valeurs de x et de y qui vérifient à la fois les deux équations.
À découvrir également : Systèmes linéaires
Résolution par substitution
La méthode par substitution consiste à exprimer dans l’une des équations, une des inconnues en fonction de l’autre et de reporter (substituer) son expression dans l’autre équation : on obtient ainsi une équation à une inconnue que l’on sait résoudre. Puis on détermine ensuite la valeur de l’autre inconnue. Cette méthode est intéressante si l’une des inconnues s’exprime de façon simple en fonction de l’autre.
Soit le système :
On calcule x en fonction de y dans la première équation, on reporte dans la deuxième équation :
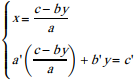
Il suffit maintenant de résoudre la deuxième équation (ne contenant que l’inconnue y) puis de calculer x.
Résoudre le système : 
On exprime x en fonction de y dans la première équation : 
On reporte dans la deuxième équation : 
Il suffit maintenant de résoudre la deuxième équation (qui est devenue une équation à une inconnue y) :
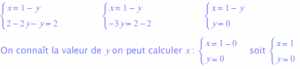
La solution est le couple ( 1 , 0 ) : S = f ( 1 , 0 ) g .
Toujours le système entier même si l’une des équations ne change pas de forme d’une ligne à l’autre.
On peut vérifier l’exactitude des résultats en reportant les valeurs trouvées pour x et y dans le système donné en énoncé.
Résolution par addition (ou combinaison)
Comme précédemment on écrit le système sous la forme :
Puis on multiplie les deux membres des deux équations ou les deux membres d’une seule des équations par un nombre tel que les coefficients de l’inconnue x (ou y) soient opposés. Puis on ajoute membre à membre les deux égalités, on élimine ainsi l’inconnue x (ou y) et on obtient une équation à une inconnue. En multipliant la première équation par a ‘ et la deuxième par -a on a :
On ajoute membre à membre les deux égalités :
la deuxième équation ne comporte que l’inconnue y.
La valeur de x s’obtient alors en remplaçant la valeur obtenue pour y dans l’une des deux équations.
Conserver l’une des deux équations du système.
On peut aussi éliminer l’inconnue y. Pour cela on multiplie la première équation par b’ et la deuxième par -b.
Résoudre le système :
On multiplie la première équation par -2 :
On ajoute membre à membre les deux égalités (l’inconnue x est ainsi éliminée) :
Pour trouver x il suffit de remplacer y par la valeur trouvée dans l’une des deux équations :
x + y = 1 avec y = 0 donne x + 0 = 1 soit x = 1. D’où l’ensemble des solutions : S = {( 1 , 0 )}.
Résolution graphique
On calcule y en fonction de x dans chacune des deux équations. On obtient un système de la forme :
où chacune des deux équations du système représente une droite.
On trace chacune de ces droites dans un repère orthonormal.
- Si ces deux droites se coupent les coordonnées du point d’intersection est le couple solution du système.
- Si les deux droites sont parallèles, elles n’ont aucun point commun : il n’y a pas de solution.
- Si les deux droites sont confondues, il y a une infinité de solutions. Les deux équations sont identiques.
Résoudre le système :
il est équivalent au système : 
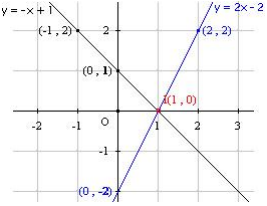
La première équation est la droite y = – x + 1 et la deuxième équation est la droite y = 2x – 2. Dans un repère orthonormal ( O , I , J) on trace ces deux droites. Le point d’intersection des droites est I de coordonnées ( 1 , 0 ). D’où la solution du système : S = {( 1 , 0 )}.