Publié le : 03 septembre 20206 mins de lecture
- Cercle circonscrit – Triangle inscrit
- Cercle circonscrit
- Définition
- Médiane
- Triangle inscrit
- Distance d’un point à une droite
- Distance entre deux points
- Définition
- Propriété :Inégalité triangulaire
- Application au triangle
- Distance d’un point à une droite
- Tangente à un cercle
- Définition
- Construire
- Construire un cercle tangent à une droite
- Position relative d’une droite et d’un cercle
- La droite et le cercle sont sécants
- La droite est tangente au cercle
- La droite est extérieure au cercle
Cercle circonscrit – Triangle inscrit
Cercle circonscrit
Définition
Tout triangle rectangle est inscrit dans un cercle dont le centre est le milieu de son hypoténuse.
Réciproque : 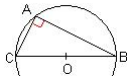
Si un triangle est inscrit dans un cercle dont un diamètre est un côté du triangle alors ce triangle est un triangle rectangle, ce côté est l’hypoténuse du triangle.
Médiane
Dans un triangle rectangle, la médiane relative à l’hypoténuse mesure la moitié de l’hypoténuse.
Réciproque : 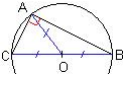
Si dans un triangle la médiane relative à un côté est égale à la moitié de la longueur de ce côté alors le triangle est rectangle et ce côté est l’hypoténuse de ce triangle.
Triangle inscrit
Si on joint un point d’un cercle aux deux extrémités d’un diamètre, alors on obtient un triangle rectangle qui admet pour hypoténuse ce diamètre.
Conséquence : 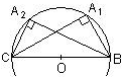
Si A est un point du cercle de diamètre [BC] alors ABC est un triangle rectangle en A.
À découvrir également : Droites remarquables du triangle
Distance d’un point à une droite
Distance entre deux points
Définition
La distance entre deux points A et B est la longueur du segment [AB]. Elle dépend de l’unité de longueur choisie.
Propriété :Inégalité triangulaire
Soient trois points A, B et C du plan, alors AB £ AC + CB
Si C n’appartient pas au segment [AB] alors AB < AC + CB. 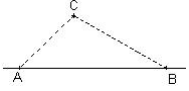
Si C appartient au segment [AB] alors AB = AC + CB.
Si AB = AC + CB, alors C appartient au segment [AB] et A, B et C sont alignés.
On utilise souvent cette propriété pour démontrer que trois points sont alignés.
Application au triangle
Dans un triangle, la somme des longueurs de deux côtés est inférieure à la longueur du troisième côté. Dans le triangle ABC on a BC ≤ AB + AC
Distance d’un point à une droite
On appelle distance du point A à la droite (d) la longueur AH où H est le point d’intersection de (d) avec la perpendiculaire à (d) passant par A. Si A appartient à la droite (d) alors A et H sont confondus et on a AH = 0. Pour tout point M de (d) autre que H on a : AM > AH. 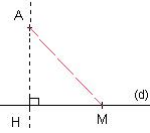
Nous vous recommandons : Angles-Rotations-Polygones réguliers
Tangente à un cercle
Définition
Soit M un point du cercle de centre O. On appelle tangente en M à ce cercle, la droite perpendicuaire en M au rayon [OM]. Une droite (d) est tangente à un cercle, de centre O et de rayon r, en H si et seulement si (OH) est perpendiculaire à (d). La distance du point O, centre du cercle, à la droite (d) est égale au rayon r du cercle.
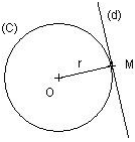
Construire
la droite tangente en un point du cercle Le point M appartient au cercle : il y a une seule tangente. On trace le rayon [OM] puis la perpendiculaire (d) en M au cercle (C). Le point M n’appartient pas au cercle : il y a deux tangentes. Le point M est à l’intérieur du cercle : il n’y a pas de tangente au cercle.
Construire un cercle tangent à une droite
Soient un point O et une droite (d) (O n’appartient pas à (d)). Tracer le cercle de centre O tangent à cette droite. On trace la perpendiculaire à (d) passant par O, puis le cercle de centre O et de rayon OM.
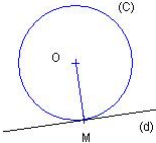
Position relative d’une droite et d’un cercle
La droite et le cercle sont sécants
La droite (d) et le cercle ont deux points communs : OM < r. En bleu sur la figure.
La droite est tangente au cercle
La droite (d) et le cercle ont un seul point commun : OM = r. En noir sur la figure. 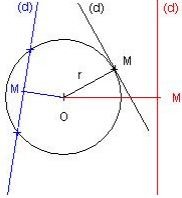
La droite est extérieure au cercle
La droite (d) et le cercle n’ont aucun point commun : OM > r.
En rouge sur la figure.
Soit une droite (d) et un point O situé à 2 cm de (d). Tracer le cercle (C) de centre O et de diamètre 4 cm.
Combien le cercle (C) et la droite (d) ont-ils de points communs ? 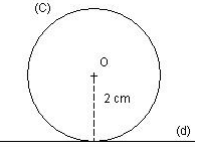
Le cercle a pour rayon 2 cm, donc le point O est situé à 2 cm de la droite (d), donc la droite (d) est tangente au cercle (C).
La droite (d) et le cercle (C) n’ont qu’un seul point commun.