Publié le : 03 septembre 20204 mins de lecture
- Relations trigonométriques dans le triangle rectangle
- Définitions
- Relations trigonométriques
- Relation fondamentale de la trigonométrie
- Relation entre cosinus, sinus et tangente
- A vos calculatrices
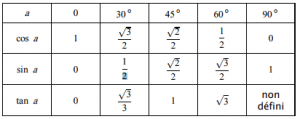
- Quelques valeurs remarquables (et courantes)
- Applications
- Calculer la longueur d’un côté dans un triangle rectangle
- Calculer la valeur des angles dans un triangle rectangle
Relations trigonométriques dans le triangle rectangle
Définitions
Soit un triangle ABC rectangle en C. Dans ce triangle on a les relations suivantes :
![]() où AC est la mesure du côté de l’angle droit adjacent à l’angle
où AC est la mesure du côté de l’angle droit adjacent à l’angle ![]() et AB la mesure de l’hypoténuse.
et AB la mesure de l’hypoténuse.
![]() où BC est la mesure du côté de l’angle droit opposé à l’angle
où BC est la mesure du côté de l’angle droit opposé à l’angle ![]() .
.
![]()
![]()
On considère l’angle ![]() , on a : On voit que :
, on a : On voit que :
![]()
- Le sinus et le cosinus d’un angle aigu sont compris entre 0 et 1.
Si deux angles sont complémentaires le sinus de l’un est égal au cosinus de l’autre :
cos α= sin (90 – α) sin α = cos (90 – α)
Relations trigonométriques
Relation fondamentale de la trigonométrie
Pour tout angle aigu de mesure a on a :
![]()
Relation entre cosinus, sinus et tangente
![]()
A vos calculatrices
Sur les calculatrices scientifiques il existe des touches ![]() ,
, ![]() ,
, ![]() qui donnent les valeurs des cosinus, sinus et tangente des angles.
qui donnent les valeurs des cosinus, sinus et tangente des angles.
Trouver la valeur du cosinus, du sinus et de la tangente d’un angle.
Mettre la calculatrice en mode degré. Afficher la valeur de l’angle dont on veut le cosinus puis presser la touche ![]() : s’affiche alors la valeur du cosinus de cet angle.
: s’affiche alors la valeur du cosinus de cet angle.
Pour calculer la valeur du sinus ou de la tangente d’un angle il faut suivre les indications précédentes en remplaçant la touche ![]() par les touches
par les touches ![]() ou
ou ![]() selon que l’on souhaite la valeur du sinus ou de la tangente.
selon que l’on souhaite la valeur du sinus ou de la tangente.
Trouver la valeur d’un angle connaissant son cosinus, sinus ou tangente
On veut trouver l’angle dont on connaît le cosinus :
On tape la valeur du cosinus :
puis les touches ![]() et
et ![]() la valeur de l’angle s’affiche alors. On procède de la même manière pour trouver la valeur d’ un angle dont on connaît le sinus ou la tangente, on remplace la touche
la valeur de l’angle s’affiche alors. On procède de la même manière pour trouver la valeur d’ un angle dont on connaît le sinus ou la tangente, on remplace la touche ![]() par la touche
par la touche ![]() ou
ou ![]() .
.
Certaines calculatrices fonctionnent différemment, se référer au mode d’emploi de votre calculatrice pour connaître la manière dont il faut procéder.
Quelques valeurs remarquables (et courantes)
Applications
Calculer la longueur d’un côté dans un triangle rectangle
Soit un triangle ABC rectangle en C. On donne AC = 4 cm et ![]()
Calculer la longueur du côté [ BC]. 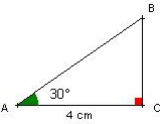
On est dans un triangle rectangle, on connaît la valeur d’un angle et la longueur du côté adjacent. Le côté cherché est opposé à l’angle. On va donc utiliser la tangente de l’angle ![]() .
.
![]() , la calculatrice donne tan 30 ± = 0,577.
, la calculatrice donne tan 30 ± = 0,577.
On a donc ![]() , d’où : BC = 4×0,577 = 2,3 cm à 0,1 cm près.
, d’où : BC = 4×0,577 = 2,3 cm à 0,1 cm près.
Calculer la valeur des angles dans un triangle rectangle
Soit un triangle ABC rectangle en C. On donne AB = 4 cm et BC = 3 cm.
Calculer la valeur de l’angle ![]()
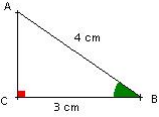
On est dans un triangle rectangle et on connaît la longueur de l’hypoténuse et
la longueur du côté de l’angle droit adjacent à l’angle cherché. On peut donc calculer le cosinus de l’angle ![]() et on a :
et on a : ![]() , la calculatrice donne :
, la calculatrice donne : ![]() = 41,409..° soit :
= 41,409..° soit : ![]() = 41,4° à 0,1° près.
= 41,4° à 0,1° près.