Publié le : 03 septembre 20205 mins de lecture
Equation linéaire à deux inconnues
ax + by = c, où a, b et c sont des réels donnés est une équation linéaire à deux inconnues (x et y). Cette équation a pour solution les couples ( x, y) de ℝ×ℝ, on écrit aussi ℝ2.
Interprétation géométrique :
Les couples ( x, y) sont les coordonnées des points de la droite (D) d’équation cartésienne ax + by – c = 0.
Systèmes linéaires à deux inconnues
Définition
![]() est un système linéaire à deux inconnues.
est un système linéaire à deux inconnues.
Interprétation géométrique
Les équations (1) et (2) sont les équations cartésiennes de deux droites (D1) et (D2 ) .
(xo ; yo) est solution si et seulement si le point Mo(xo ; yo) appartient à la fois aux droites (D1) et (D2).
Solutions du système
Plusieurs cas peuvent se produire :
- Les droites (D1) et (D2) sont sécantes, dans ce cas il y a une et une seule solution, le point d’intersection des
droites (D1) et (D2). - Les droites (D1) et (D2) sont parallèles :
Si les droites (D1) et (D2) sont strictement parallèles, alors elles n’ont aucun point commun et le système
n’a pas de solution.
Si les droites (D1) et (D2) sont confondues, alors le système admet une infinité de solutions, tous les
points des droites (D1) et (D2).
Méthodes de résolution
On recherhe d’abord si le système a des solutions, c’est à dire qu’on calcule le nombre ab’ – ba ‘ :
- Si ab’ – ba ‘ ≠ 0 alors le système a une solution unique.
- Si ab’ – ba ‘ = 0 alors le système n’a pas de solution ou a une infinité de solutions. On résout ensuite le système par l’une des méthodes ci-dessous :
Substitution
On exprime x en fonction de y dans l’une des deux équations (ou bien y en fonction de x) et on remplace dans la
deuxième équation. On obtient ainsi une équation à une inconnue.
Combinaison (ou addition)
On élimine l’une des inconnues x ou y en combinant les deux équations. Pour cela on peut :
- multiplier les deux membres d’une ou des deux équations par un même nombre non nul;
- ajouter ou retrancher membre à membre les deux équations.
Comparaison
On exprime l’une des deux inconnues en fonction de l’autre dans chacune des deux équations. Les expessions
obtenues doivent être égales, donc par comparaison on obtient une équation a une inconnue.
Résolution graphique
On trace les deux droites (D) et (D’) correspondant aux équations (1) et (2) du système.
(D)⋂(D’) = M, le système a une seule solution : les coordonnées du point M.
(D)⋂(D’) = Ø, le système n’a aucune solution.
(D)⋂(D’) = (D) = (D’), le système une infinité de solutions, tous les points de la droite (D) (ou (D’)).
Résoudre graphiquement le système ![]()
L’équation 2x + 3y = – 4 ⇔ ![]() .
. 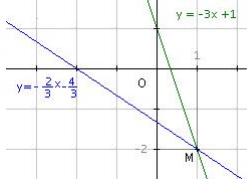
L’équation 3x + y = 1 , y = – 3x + 1. Dans un même repère on trace les droites d’équation ![]() et y = – 3x + 1.
et y = – 3x + 1.
Les droites se coupent en M( 1 ; – 2 ). La solution unique du système est S = {( 1 ; – 2 )}.
Mettre en équation un problème
Méthode
En lisant l’énoncé déterminer les inconnues et préciser l’ensemble auquel elles appartiennent.
Traduire chaque information de l’énoncé par une équation faisant intervenir les inconnues choisies. Résoudre le système obtenu en appliquant l’une des méthodes décrites plus haut.
Vérifier si les solutions trouvées sont compatibles avec les conditions imposées par le problème. Conclure par une phrase répondant aux questions posées dans l’énoncé.
Exemple
Un rectangle est tel que :
- si on augmente sa longueur de 7 m et si on diminue sa largeur de 5 m, son aire est inchangée ;
- si on augmente sa longueur de 20 m et si on diminue sa largeur de 13 m, son aire augmente de 20 m 2 .
Calculer les dimensions d’un tel rectangle.
Soit x et y la longueur et la largeur respectives du rectangle. Son aire est xy.
La première condition de l’énoncé donne : (x + 7)(y – 5) = xy
La deuxième condition donne : (x + 20)(y – 13) = xy + 20
D’où le système : ![]()
La solution du système est x = 140 et y = 105.
x et y représentent des longueurs, on a trouvé des nombres positifs, donc ces valeurs conviennent.
Le rectangle a une longueur de 140 m et une largeur de 105 m.