Statistiques

Publié le : 29 janvier 20189 mins de lecture

Définitions

Etude d’une population

• La couleur des yeux, des cheveux sont des variables qualitatives variables qualitatives variables qualitatives , on parle de modalité modalité modalité.
• La taille est une valeur quantitative valeur quantitative valeur quantitative , dans ce cas on parle de variable.
• Variable continue , la variable peut prendre toutes les valeurs de ℝ, par exemple la taille des élèves. Variable continue
• Variable discrète , la variable ne peut pas prendre toutes les valeurs, par exemple la pointure, le nombre de frères Variable discrète et sœurs. On ne peut pas avoir 1,3 frères et sœurs !

Effectif

Pour une valeur, c’est le nombre d’individus possédant le caractère étudié.

Exemple : Le nombre d’élèves ayant des cheveux blonds.

La somme de tous les effectif est l’effectif total effectif total effectif total c’est l’ensemble de la population étudiée.

Fréquence

C’est le quotient de l’effectif de la valeur sur l’effectif total. Elle est donnée soit en pourcentage ( % ) soit par un
nombre compris entre 0 et 1.

La somme des fréquences est égale à 1 ou 100%.

Effectifs cumulés – Fréquence cumulées

S’obtiennent en ajoutant au fur et à mesure les effectifs (respectivement les fréquences) des valeurs précédentes.

Exemple : Notes obtenues à un contrôle. L’effectif cumulé pour la note n est le nombre d’élèves ayant obtenu une
note inférieure ou égale à n.

Série statistique à une variable

Exemples de calculs

On étudie les 30 élèves d’une classe d’un lycée.

Exemple 1

Nombre de frères et sœurs des 30 élèves.

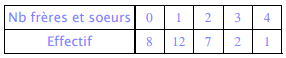
Le nombre de frères et sœurs est un caractère numérique discret.

Exemple 2

Poids des 30 élèves.

Le poids est un caractère numérique continu.

Étendue

C’est la différence entre les valeurs extrêmes du caractère.

Exemple 1 : L’étendue est Exemple 1 4 − 0 = 4

Exemple 2 : L’étendue est Exemple 2 65 − 40 = 25

Mode ou classe modale

C’est la valeur du caractère correspondant à l’effectif le plus grand.

Exemple 1 : Le mode est Exemple 1 1 car il correspond à l’effectif maximum 12.

Exemple 2 : La classe modale est ]55; 60] car elle correspond à l’effectif maximum 9.

Médiane

C’est la valeur du caractère séparant la population en deux groupes de même effectif.

C’est donc le nombre pour lequel l’effectif cumulé est égal à la moitié de l’effectif total.

La médiane correspond donc à une fréquence cumulée de 0,5 (ou un pourcentage cumulé de 50%).

Exemple 1 : La médiane est Exemple 1.

En effet l’effectif cumulé pour la valeur 1 est égal à 8 + 12 = 20, la moitié de l’effectif total (15) est atteint pour la valeur 1.

Exemple 2 : La médiane est ] 50; 55].

En effet pour cette classe l’effectif cumulé est égal à 3 + 6 + 7 = 16, la moitié de l’effectif total (15) est atteint pour la classe ]50; 55].

Moyenne arithmétique

Soit N = n₁+ n₂+ ……n_p l’effectif total et x₁, x₂ … x_p les valeurs correspondantes aux effectifs partiels.

La moyenne arithmétique de la série est le réel noté , défini par : 

On appelle   les fréquences correspondantes, donc : = f₁ x₁ + f₂ x₂… f_p x_p

Linéarité de la moyenne

• Si on multiplie toutes les valeurs de la série par un même réel a, la moyenne est multipliée par a.
• Si on ajoute à toutes les valeurs de la série un même réel b, la moyenne est augmentée de b.

Moyennes partielles

Soit et les moyennes de deux parties d’une série d’effectifs n et p, alors la moyenne de la série est la moyenne des moyennes partielles et affectées respectivement des effectifs n et p : 

Distribution de fréquences

Soit un caractère numérique discret. La distribution de fréquences de la série est la donnée du tableau :

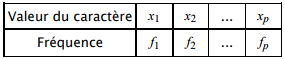
On a f₁ + f₂ + … + f_p = 1

Représenter graphiquement une série statistique

Diagramme bâtons

Exemple 1

En abscisses on a le nombre de frères et sœurs et en ordonnées les effectifs.

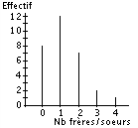
Les échelles sur chaque axe sont indépendantes.

Histogramme

Exemple 2

En abscisses on a les intervalles de poids et en ordonnées les effectifs.

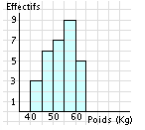
L’aire des rectangles est proportionnelle à l’effectif

Effectuer des calculs à la calculatrice

Calculer une moyenne en utilisant les fonctions statistiques de la calculatrice. Dans la plupart des calculatrices, les calculs de la moyenne sont pré-programmés.

Procédure générale

a. Mettre la calculatrice en « mode statistique » et effacer les mémoires à l’aide de la touche « Scl »
b. Entrer les valeurs des caractères et les effectifs correspondants à laide de la touche « DATA » (ou « DT »)
c. Calculer la moyenne à l’aide de la touche « « .

Effectuer des simulations

La fonction « Random » de la calculatrice

La fonction Random est accessible par la touche « Ran# » ou « rand » selon les calculatrices. Cette fonction génère des nombres aléatoires uniformément répartis dans l’intervalle [0; 1[.

Simulations

L’utilisation des nombres aléatoires permet de simuler un grand nombre de situations, par exemple, le lancer d’une pièce de monnaie ou le tirage de boules dans une urne.

Pour simuler le jet d’une pièce de monnaie on peut générer un nombre aléatoire et considérer que tout nombre inférieur à 0,5 est Pile et tout nombre supérieur à 0,5 est Face.

Principe du programme

On génère un nombre aléatoire, si le nombre est inférieur à 0,5, on assimile le résultat à Pile. On ajoute alors 1 à la variable P (Pile) et on mémorise le résultat dans P. L’instruction s’écrit P + 1 → P.

Si le nombre est supérieur à 0,5, on procède de la même façon avec la variable F (Face).

Il faut initialiser les variables P et F à 0 en début de programme.

La répétition des lancers est gérée par une « boucle For » : demande le nombre de lancers.

Etapes du programme

0 → F : 0 → P                                                                                          (initialisation à 0 des variables F et P)
100 → J                                                                                                     (entrer le nombre de lancers à effectuer : 100)
For 1 → I to J                                                                                            (boucle For)
if Ran# < 0.5 : Then P + 1 → P                                                              (comptabilisation Else F + 1 → F des résultats)
Next                                                                                                             (fin de la boucle For)
« NB FACE= »F                                                                                            (affichage du nombre de Face)
« NB PILE= »P                                                                                              (affichage du nombre de Pile)
« FREQ FACE= »F/J                                                                                    (affichage de la fréquence de Face)
« FREQ PILE= »P/J                                                                                     (affichage de la fréquence de Pile)