Publié le : 29 janvier 20188 mins de lecture
Sphère et boule
Définitions
La sphère de centre La sphère O et de rayon R est l’ensemble des points M de l’espace tels que OM = R : la distance de M à O est égale à R.
La boule de centre La boule O et de rayon R est l’ensemble des points M de l’espace tels que OM ≤ R : la distance de M à O est inférieure ou égale à R.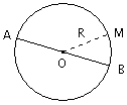 
Diamètre d’une sphère : toute droite passant par son centre. Une telle droite coupe la Diamètre sphère en deux points A et B.
Intersection d’une sphère et d’un plan
La section d’une sphère par un plan est un cercle. Le plan de section est perpendiculaire en H au diamètre [ ] AB de la sphère et on a : OH = h.
Le centre du cercle de section est H. Soit M un point de ce cercle et r son rayon, on a alors HM = r.
Calcul du rayon du cercle de section
La droite ( ) OH est perpendiculaire au plan contenant le cercle de section. Donc le triangle OHM est rectangle en H. Le point M appartient à la sphère, donc OM = R.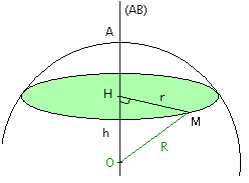 
Le théorème de Pythagore appliqué au triangle OHM donne :
OM2= OH2 + HM2
Avec OM = R, OH = h et HM = r on a
R2= h2+ r2d’où :
r2= R2− h2
Il faut savoir faire ce calcul.
a. si 0 < h < R alors r < R on a un cercle de centre H et de rayon r < R.
b. si h = 0 alors r = R : H et O sont confondus on a un cercle de centre O et de rayon R. On l’appelle grand cercle grand cercle grand cercle de la sphère : intersection d’une sphère avec un plan diamétral.
c. si h = R alors r = 0 alors H et A (ou B) sont confondus on a un point : A (ou B). L’intersection de la sphère et du plan se réduit à un point.
d. si h > R alors le plan P ne coupe pas la sphère. Il n’y a aucun point commun entre la sphère et le plan.
Aire et volume
Aire d’une sphère de rayon R : A = 4πR2
Volume d’une sphère de rayon R : V = (4/3)πR3
La Terre
On assimile la terre à une boule dont le rayon est voisin de 6370 km. Dans les calculs on arrondit souvent à 6400
km.
Sa circonférence à l’équateur est donc de : 2π×6370 ≃ 40000 km.
Vocabulaire particulier à la Terre :
méridien : demi-cercle à la surface de la Terre allant d’un pôle à l’autre.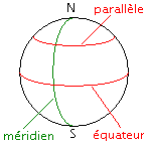 
Les méridiens sont repérés de part et d’autre d’un méridien origine : le méridien de Greenwich qui passe dans la banlieue de Londres.
parallèle : cercle faisant le tour de la Terre parallèle à l’équateur parallèle équateur équateur.
Repérage d’un point sur la Terre
Un point est repéré par sa longitude longitude longitude et sa latitude latitude latitude exprimées en degrés.
La longitude du point M est l’angle est l’angle 
et la latitude du point M est l’angle 
.
Pour la longitude on précise Est ou Ouest : l’origine étant le méridien de Greenwich.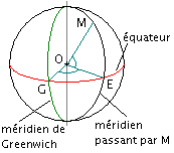 
Pour la latitude on précise Nord ou Sud : l’origine étant l’équateur.
Tous les points de même longitude sont sur le même méridien.
Tous les points de même latitude sont sur le même parallèle.
Sections panes de solides
Parallélépipède rectangle
La section d’un parallélépipède rectangle par un plan parallèle à une de ses faces est un rectangle égal à cette parallèle à une de ses faces face. (figure1)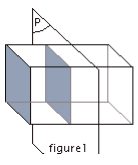 
La section d’un parallélépipède rectangle par un plan parallèle à une de ses arrêtes est un rectangle dont deux parallèle à une de ses arrêtes côtés ont même longueur que cette arrête. (figure2)
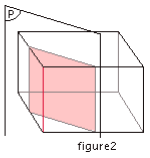
Cylindre de révolution
La section d’un cylindre par un plan parallèle à ses bases plan parallèle à ses bases est un cercle de même rayon que la base et dont le centre appartient à son axe. (figure1)
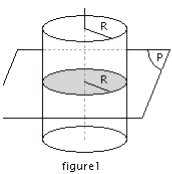
La section d’un cylindre par un plan parallèle à son axe plan parallèle à son axeest un rectangle dont deux côtés ont même longueur que sa hauteur. (figure2)
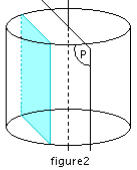
Si le plan contient l’axe du cylindre alors le rectangle aura pour longueur la hauteur du cylindre et pour largeur le diamètre de la base.
Pyramide
La section d’une pyramide par un plan parallèle à sa base plan parallèle à sa base est un polygone de même forme que la base. (figure1)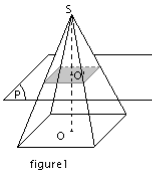 
Ses côtés sont parallèles à ceux de la base.
Cône de révolution
La section d’un cône par un plan parallèle à sa base plan parallèle à sa base plan parallèle à sa base est un cercle dont le centre appartient à l’axe du cône. (figure2)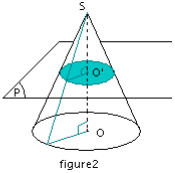 
Rapport de réduction
La section d’une pyramide ou d’un cône de révolution par un plan parallèle à la base est une réduction du polygone ou du cercle de base.
Le rapport 
est le rapport de réduction rapport de réduction rapport de réduction .
Aires et Volumes
Parallélépipède et cube
Aire latérale : somme des aires des 4 faces qui sont des rectangles dans le cas du parallélépipède et des carrés dans le cas du cube.
parallélépipède de dimensions L×l×h : A = 2Lh + 2lh = 2h(L+ l)
cube d’arrête a : A = 4a2
Volume :
du parallélépipède de dimensions L×l×h on a : V = L×l×h
du cube d’arrête a on a : V = aX3
Cylindre
Aire latérale : A = 2π Rh
Volume : V = πR2h
Pyramide
Aire latérale : Somme des aires des triangles isocèles qui forment la pyramide.
Aire de la base : dépend de la forme de la base : triangle, carré, rectangle, polygone à n côtés : B
Volume : V =(1/3)Bh
Cône
Aire latérale : A = π Ra (où a est l’apothème, a2= h2+ R2)
Aire de la base : B = πR2
Volume : V = (1/3)πR2h
Le volume de la pyramide et du cône s’expriment de la même façon si on appelle B l’aire de la base : V =(1/3)Bh
Sphère
Aire : A = 4πR2
Volume : V =(4/3)πR3