Géométrie dans l’espace

Publié le : 29 janvier 20187 mins de lecture

Positions relatives de droites et plans

A. Position relative de deux droites

Soient deux droites (D) et (D’)  :
(D) et (D’)  sont coplanaires c’est à dire contenues dans le même plan, elles sont : sont coplanaires

• soit sécantes en un point (D) ∩(D’) =  M
• soit parallèles (D)∩(D’) = Ø                                                          
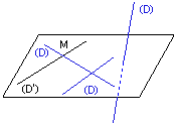
• soit confondues (D) ∩(D’) = (D) = (D’)

(D) et (D’) ne sont pas coplanaires c’est à dire non contenues dans un même plan. Il n’y a aucun point commun entre elles (D)∩(D’) = Ø.

Position relative de deux plans

Les plans (P) et (P’) sont sécants.
L’intersection des deux plans est une droite.
(P) ∩(P’) = (∆)

Les plans (P) et (P’) sont parallèles.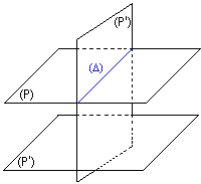                               
(P) ∩(P’) = Ø

Les plans (P) et (P’) sont confondus.
(P) ∩(P’) = (P) = (P’)

Position relative d’une droite et d’un plan

La droite (D) est incluse dans le plan (P) : (D) ⊂ (P)
(D) ∩(P) = (D)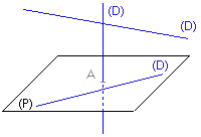                                                                                     

La droite (D) n’est pas incluse dans le plan (P) : (D) ⊄ (P)

• La droite (D) coupe le plan (P) : (D) ∩(P) = A
• La droite (D) ne coupe pas le plan (P) : (D) ∩(P) = Ø
  (D) et (P) n’ont pas de point commun.

Règles d’incidence

Pour que des plans (P) et (P’) soient parallèles, il faut et il suffit que deux droites sécantes de (P) soient parallèles à deux droites sécantes de (P’).
(D)//(D’) et (∆)//(∆’) ⇔ (P)//(P’)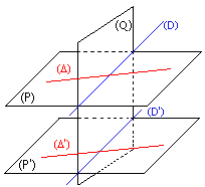                                                

Théorème d’incidence

Si deux plans sont parallèles, tout plan qui coupe l’un coupe l’autre et les droites d’intersection sont parallèles.
Si (P)//(P’) et (P)∩(Q) =(D), alors (Q)∩(P’) = (D’) et (D)//(D’).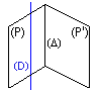                         

Si deux plans sécants (P) et (P’) sont parallèles à une même droite (D), alors leur intersection est une droite (∆) parallèle à (D).

Si (D) // (P) et (D) // (P’), alors (P) ∩(P’) = (∆) et (∆) // (D)

Orthogonalité dans l’espace

Droites orthogonales

Définition

Deux droites (D) et (D’) de l’espace sont orthogonales, si et seulement si, les parallèles à (D) et (D’) menées par un même point M sont perpendiculaires.

Propriétés

• Si deux droites sont perpendiculaires, alors toute parallèle à l’une est perpendiculaire à l’autre.
• Si deux droites sont parallèles, alors toute perpendiculaire à l’une est parallèle à l’autre.

(AB) ⊥ (CG), en effet :
(FB) ⊥ (AB) or (FB) // (CG), donc (AB) ⊥ (CG).

(EH) ⊥ (FB) et (FB) // (CG)  donc (EH) ⊥ (CG)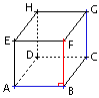                               
(EH) // (BC) et (EA) ⊥ (EH) donc (EA) ⊥ (BC)

Orthogonalité d’une droite et d’un plan

Définition

Une droite (D) est orthogonale à un plan (P) si et seulement si elle est orthogonale à toutes les droites du plan. Pour qu’une droite (D) soit orthogonale à un plan (P), il faut et il suffit qu’elle soit orthogonale à deux droites sécantes du plan.

Si une droite est orthogonale à un plan, alors elle est orthogonale à toutes les droites du plan.

Propriétés

Si un plan (P) est orthogonal à une droite (D) et coupe cette droite en un point M, alors toute droite passant par M et orthogonale à (D) est dans le plan (P).

Si deux droites sont parallèles, alors tout plan orthogonal à l’une est orthogonal à l’autre.
Si deux droites sont orthogonales à un même plan, alors elles sont parallèles.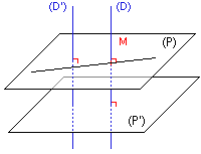                            
Si deux plans sont parallèles, alors toute droite orthogonale à l’un est orthogonale à l’autre.
Si deux plans sont orthogonaux à une même droite, alors ils sont parallèles.
Un point M et un plan (P) étant donnés, il existe une droite (D) unique passant par M et orthogonale à (P).
Un point M et une droite (D) étant donnés, il existe un plan (P) unique passant par M et orthogonal à (D).

Aires et volumes de solides usuels

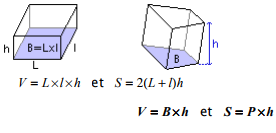
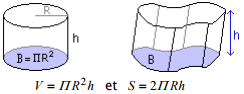
Dans les formules suivantes, V désigne le volume, S la surface latérale, B la surface de base et P le périmètre de la base.

Parallélépipède rectangle – Prisme

Cylindre de révolution – Cylindre quelconque

Pyramide – Cône

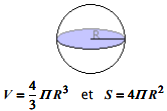
Sphère

Perspective cavalière

Principes de la perspective cavalière

Les faces d’un solide, représenté en perspective cavalière, parallèles à la feuille gardent la même forme.
Les droites orthogonales à la feuille sont représentées obliquement et restent parallèles entre elles. Les distances sont réduites d’un même coefficient.
Les faces ABFE et DCGH sont des carrés car elles sont parallèles à la feuille.
Les droites (EH), (FG), (BC) et (AD) sont perpendiculaires à la feuille et parallèles entre elles. On a EH = FG = BC = AD = kAB avec 0 < k < 1.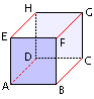                                                     
Les faces BCGF et ADHE sont représentées par des parallélogrammes.
Les arêtes cachées sont tracées en pointillé.
Ce type de représentation conserve le parallélisme.

Exemple

Soit le cube ABCDEFGH, représenter le prisme ACDEGH en perspective cavalière avec la face EGH dans le plan de la feuille de papier, le côté [EG] étant horizontal.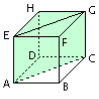                         

Méthode

On construit le triangle EGH rectangle en H et isocèle : EH = GH. Ce triangle est dans le plan de la feuille donc il reste rectangle isocèle.

Les droites (HD), (EA) et (GC) sont perpendiculaires au plan (EGH), donc on les représente par des droites obliques et parallèles entre elles avec HD = EA = GC.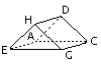                                        

On trace ensuite les arêtes [AD] et [AC] et [EA] en pointillé.