Publié le : 29 janvier 20185 mins de lecture
Définitions
La fonction f est la relation qui associe à un nombre x d’un ensemble D un nombre unique y, image de x . On note f : x ↦ y ou y = f( x) ou f : x ↦ f( x)
Domaine de définition
Le domaine de définition D de la fonction f est l’ensemble des nombres x qui ont une image f( x).
x ∈ D
Courbe représentative
Soit f une fonction définie sur D par f : x ↦ f( x)
Dans un repère ( O, I, J) la courbe représentative de f est l’ensemble des points M( x ; f( x) ).
Images et antécédents
f( x) est l’image de x par f, l’image est unique. x est un antécédent de f( x), il peut y avoir plusieurs antécédents. En abscisses on trouve x et en ordonnées on trouve f( x).
Déterminer une image ou un antécédent par le calcul :
Pour calculer l’image de x = a, il suffit de calculer y = f( a). Pour calculer les antécédents de c, il suffit de résoudre l’équation f( x) = c.
Soit la fonction f( x) = x2 – 5 définie sur ℝ. Déterminer les antécédents de 4.
Dans ce cas on a f( x) = 4, soit x2 – 5 = 4 ⇔ x2 – 5 – 4 = 0 ⇔ x2 – 9 = 0 ⇔ ( x – 3 )( x + 3 ) = 0
Cette équation a deux solutions : x – 3 = 0 et x + 3 = 0
4 a deux antécédents 3 et -3 .
Sens de variation
Définitions
Soit f une fonction définie sur un intervalle I.
- La fonction f est croissante sur I si et seulement si a £ b alors f( a) £ f( b).
- La fonction f est décroissante sur I si et seulement si a £ b alors f( a) ³ f( b).
- La fonction f est « constante » si tous les éléments de I ont la même image.
Sur la figure ci-contre soit la fonction f définie sur
l’intervalle [ -2; + 1 ]. Sur l’intervalle [ -2; 1 ] la fonction f est croissante
Sur l’intervalle [ 1; 3 ] la fonction f est décroissante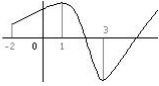 
Sur l’intervalle [ 3; + 1 ] la fonction f est croissante.
Tableau de variation
On résume les sens de variation d’une fonction dans un tableau de variation. Le tableau donne l’allure de la courbe. Dans l’exemple ci-dessus on a :
Extrémuns
Soit une fonction f définie sur I et x₀ ∈ I. La fonction f présente un maximum en x₀ si et seulement si pour tout x appartenant à I f(x) ≤ f(x₀)
La fonction f présente un minimum en x0 si et seulement si pour tout x appartenant à I f(x) ≥ f(x₀)
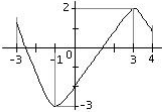La fonction f est définie sur [ -3; 4 ] et présente un minimum en ( -1; – 3 ) et un maximum en ( 3; 2 ).
Propriétés des fonctions
Parité
Soit f une fonction définie sur un ensemble D :
f est paire si et seulement si : pour tout x ∈ D alors -x ∈ D et f(-x) = f(x). Dans un repère orthonormal ( O, I, J), la courbe représentative de f est symétrique par rapport à l’axe des ordonnées.
f est impaire si et seulement si : pour tout x ∈ D alors -x 2 D et f( -x) = – f( x). Dans un repère orthonormal ( O, I, J), la courbe représentative de f est symétrique par rapport à l’origine du repère.
Construction d’une courbe représentative point par point
- On repère les maxima et les minima de la fonction.
- On cherche les sens de variation.
- On dresse un tableau de variation.
- On calcule quelques points sur les différents intervalles.
Résolution graphique d’équations/inéquations
Equation
- f ( x ) = 0
Les solutions sont les abscisses des points d’intersection de la courbe représentative de la fonction f avec l’axe des abscisses.
- f ( x ) = k
Les solutions sont les abscisses des points d’intersection de la courbe représentative de la fonction f avec la droite d’équation y = k.
- f ( x ) = g ( x )
Les solutions sont les abscisses des points d’intersection de la courbe représentative de la fonction f avec la courbe représentative de la fonction g.
Inéquation
- f ( x ) > 0
Les solutions sont les abscisses des points de la courbe représentative de la fonction f qui sont situés au dessus de l’axe des abscisses.
- f ( x ) > k
Les solutions sont les abscisses des points de la courbe représentative de la fonction f dont l’ordonnée est supérieure à k.
- f ( x ) > g ( x )
Les solutions sont les abscisses des points de la courbe représentative de la fonction f situés au-dessus de la courbe représentative de la fonction g.