Publié le : 29 janvier 20184 mins de lecture
Fonctions affines
Définitions
Soient a et b deux réels. La fonction f définie sur ℝ par f( x) = ax + b est une fonction affine. a est appelé coefficient directeur ou pente et b est l’ordonnée à l’origine.
Dans un repère, la représentation graphique de f : x ↦ ax + b est la droite ( D) de coefficient directeur a et passant par le point P( 0 ; b). y = ax + b est appelée équation réduite de ( D).
Déterminer une fonction affine
Une fonction affine est déterminée par la donnée de deux nombres et de leurs images. Soit une fonction affine définie sur ℝ, telle que f( 2 ) = 2 et f( -2 ) = 4. Déterminer f. f est une fonction affine, donc il existe deux nombres a et b tels que pour tout x, f( x) = ax + b.
f( 2 ) = 2a + b = 2 et f( -2 ) = – 2a + b = 4
Le couple ( a ; b) vérifie le système :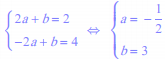 
D’où la fonction affine f ( x ) = – 1/2 x + 3
Propriétés des fonctions affines
Soit la fonction affine f(x) = ax + b définie sur ℝ. Soient x₁ et x₂ deux nombres distincts.
f(x₁) = ax₁ + b et f(x₂) = ax₂ + b, alors 
ou encore 
f est une fonction affine si et seulement si l’accroissement y₂ – y₁ de l’image est proportionnel à l’accroissement x₂ – x₁ de la variable. Si f(α) = β alors f(x) = α(x – α) + β
f( x) = 0 pour x = –
, la courbe représentative coupe l’axe des abscisses en –.
Sens de variation :
a > 0 , f est strictement croissante sur ℝ.
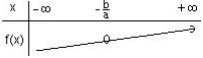
a < 0 , g est strictement décroissante sur ℝ.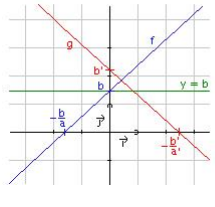 
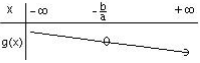
a = 0 alors f( x) = b est une fonction constante.
Résoudre une inéquation
Soient f et g deux fonctions affines définies sur ℝ par : f( x) = – 2x + 5 et g ( x) =(2/3) x+ 2
a. A l’aide de la représentation graphique de f, résoudre f( x) ≥ 0.
b. Résoudre graphiquement l’inéquation f( x) < g ( x).
- f( x) ≥ 0 ⇔ – 2x + 5 ≥ 0 , x ≤ (5/2)
Cela correspond à la portion de la droite Cf située au-dessus de l’axe des abscisses.
La solution de l’inéquation est : S = ]-1; 5/2]
- f( x) < g ( x) ⇔ – 2x + 5 < (2/3) x + 2
La solution de cette inéquation est x > (11/8)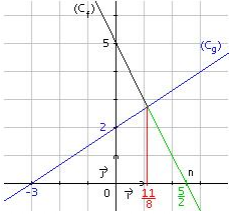 
Cela correspond à la portion de la droite Cf située au-dessous de la droite Cg. En vert sur la figure.
Les solutions sont : S = [11/8; + 1[
Fonctions linéaires
Définition
Une fonction linéaire est une fonction définie sur ℝ par f( x) = ax, où a est un réel. Sa représentation graphique est une droite passant par l’origine du repère. Une fonction linéaire est croissante si a > 0 et décroissante si a < 0.
Exemples de fonctions linéaires
Vitesse
t ↦ vt ou encore d = vt est une fonction linéaire de coefficient directeur v. On a aussi t = (1/v) d alors t est une fonction linéaire de coefficient directeur (1/v)
et on a d ↦(1/v)d
Pourcentages
On augmente ou on diminue par exemple le prix d’un article de p%
Augmentation
f( x) = x +(px/100) =(( 100 + p)/100)x Le coefficient directeur est ( 100 + p)/100
Diminution
f( x) = x -(px/100) =(( 100 – p)/100) x Le coefficient directeur est ( 100 – p)/100
Périmètre
Carré de côté a : P = 4a est une fonction linéaire de coefficient directeur 4. Cercle de rayon R : P = 2π R est une fonction linéaire de coefficient directeur 2π .