Publié le : 03 septembre 20203 mins de lecture
Médiatrices
Médiatrice d’un segment
La médiatrice d’un segment est la droite perpendiculaire à ce segment en son milieu.
Si M est un point de la médiatrice du segment [ AB] alors MA = MB.
Réciproquement, si MA = MB alors le point M appartient à la médiatrice du segment [ AB].
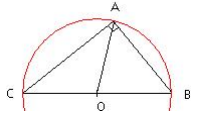
Médiatrices du triangle
Les médiatrices des trois côtés d’un triangle sont concourantes en un seul et même point qui est le centre du cercle circonscrit au triangle.
[ OA], [ OB], [ OC] sont des rayons du cercle circonscrit.
OA = OB = OC = r
À découvrir également : Triangle rectangle : cercle et distance
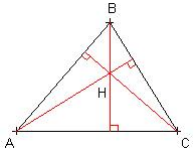
Hauteurs
Définition
Dans un triangle, on appelle hauteur une droite qui passe par un sommet et qui est perpendiculaire au côté opposé.
Orthocentre
Les trois hauteurs d’un triangle sont concourantes en un seul et même point qui est l’orthocentre de ce triangle. Si les trois angles du triangle sont des angles aigus, l’orthocentre est à l’intérieur du triangle. Si le triangle a un angle obtus, l’orthocentre est à l’extérieur du triangle. Si le triangle ABC est rectangle en B alors B est son orthocentre.
Bissectrices
Bissectrice d’un angle
La bissectrice d’un angle est la droite qui partage cet angle en deux angles de même mesure. C’est l’axe de symétrie de l’angle.
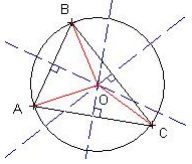
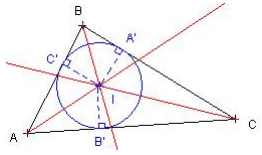
Centre du cercle inscrit
Les bissectrices des trois angles d’un triangle se coupent en un seul et
même point qui est le centre du cercle inscrit dans le triangle. Le cercle inscrit est tangent aux trois côtés du triangle.
[ IA’], [ IB’], [ IC’] sont des rayons du cercle inscrit.
Médianes
Définition
Dans un triangle, on appelle médiane un segment qui joint un sommet et le milieu du côté opposé.
Centre de gravité
Les trois médianes d’un triangle se coupent en un seul et même point qui est le centre de gravité du triangle.
Propriété :
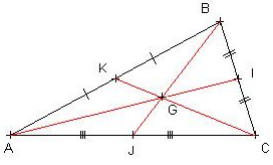
Le centre de gravité G est situé aux 2/3 de chacune des médianes à partir du sommet :
Soit I, J et K les milieux des côtés du triangle ABC :
Triangles particuliers
Triangle isocèle
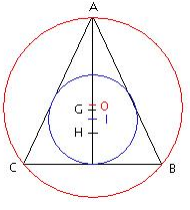
Dans un triangle isocèle, la hauteur, la bissectrice, la médiane issue du sommet principal et la médiatrice du côté opposé au sommet principal sont confondues. Les points H, I, G et O sont alignés avec le sommet principal A.
Triangle équilatéral
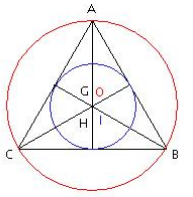
Dans un triangle équilatéral, le centre du cercle inscrit, l’orthocentre, le centre du cercle circonscrit et le centre de gravité sont confondus. On dit aussi que les bissectrices sont aussi hauteurs, médianes et médiatrices. Les points H, I, G et O sont confondus.
 Triangle rectangle
Triangle rectangle
Dans un triangle rectangle, le centre O du cercle circonscrit est le milieu de l’hypoténuse, l’orthocentre est le sommet de l’angle droit du triangle et les deux côtés de l’angle droit sont des hauteurs du triangle.