Publié le : 29 janvier 20184 mins de lecture
Le triangle
Droites remarquables du triangle
Les trois médiatrices d’un triangle sont concourantes en un point O : le centre du cercle circonscrit au triangle.
Les trois médianes d’un triangle sont concourantes en un point G : le centre de gravité du triangle.
Le point G est situé aux 2/3 de chacune des médianes du triangle.
Les trois hauteurs d’un triangle sont concourantes en un point H : l’orthocentre du triangle.
Les trois bissectrices d’un triangle sont concourantes en un point I : le centre du cercle inscrit dans le triangle.
Le cercle inscrit est tangent aux trois côté du triangle ABC.
Dans un triangle il y a aussi 3 bissectrices extérieures et 3 triangles exinscrits.
Triangles particuliers
Droite d’Euler : Dans un triangle quelconque l’orthocentre H, le centre de gravité G et le point de concours des
médiatrices O sont alignés sur une droite nommée la droite d’Euler.
Dans un triangle isocèle les points 0, G, H et I sont sur une même droite. Cette droite est à la fois médiatrice, médiane, hauteur et bissectrice.
Dans un triangle équilatéral Les points 0, G, H et I sont confondus. Toutes les médiatrices sont aussi médianes, hauteurs et bissectrices.
Un triangle rectangle est inscriptible dans un cercle dont le diamètre est son hypoténuse. La médiane relative à l’hypoténuse est égale à la moitié de l’hypoténuse.
Le triangle rectangle
Théorème de Pythagore
Si un triangle ABC est rectangle en A alors on a AB² + AC² = BC²
et réciproquement :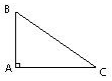 
Si dans un triangle on a AB² + AC² = BC² alors ce triangle est rectangle en A et [ BC] est son hypoténuse.
Relations trigonométriques dans le triangle rectangle
Dans le triangle ABC rectangle en A ci-dessus on a les relations suivantes :
Théorème de Thalès
Soient deux droites ( D) et ( D’) sécantes en A, deux points B et B’ de ( D) et deux points C et C’ de ( D’).
Enoncé :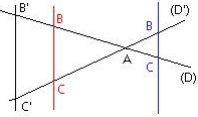 
Si les droites ( BC) et ( B’C’) sont parallèles alors 
Réciproque :
Si 
et les points A, B, B’ et A, C, C’ sont dans le même ordre alors les droites ( BC) et ( B’C’) sont parallèles.
Polygones
Un quadrilatère est un polygone possédant quatre côtés. Un polygone régulier a tous ses côtés de même longueur et tous ses angles égaux.
Les triangles équilatéraux et les carrés sont des polygones réguliers. Les trapèzes, les parallélogrammes, les losanges et les rectangles ne sont pas des polygones réguliers.
Angles et cercles
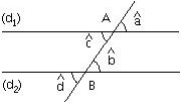
Angles correspondants – Angles alternes-internes
Si ( d1) / / ( d2 ) alors :
Angles inscrits – Angles au centre
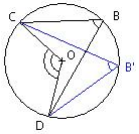
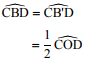
- deux angles inscrits interceptant le même arc sont
égaux. - un angle inscrit vaut la moitié de l’angle au centre
correspondant.
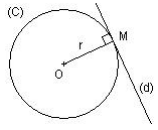
La tangente à un cercle en un point est la droite perpendiculaire au rayon du cercle en ce point.
La droite (d) est tangente en M au cercle (C) de rayon r si et seulement si (OM) ⊥ (d) et OM = r
